[TOC]
相关操作
输入操作
public class Test03 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("1.录入信息 0.退出");
int n = scanner.nextInt();
System.out.println("请输入姓名：");
String str = scanner.nextLine();
System.out.println("请输入年龄：");
int age = scanner.nextInt();
}
}
可以看到nextLine()自动读取了被next()去掉的Enter作为他的结束符，所以没法给str 从键盘输入值。 double nextDouble(),float nextFloat(),int nextInt()等与nextLine()连用时都存在这个问题。
遍历字符串
for(int i = 0 ; i < str.length();i++){
char c = str.charAt(i);
}
int[] strs = new int[26];
for(char c : str.toCharArray()){
strs[c-'a']++;
}
字母数组存储
funr storeStr(String str){
int[] letter = new int[26];
for(int i = 0 ; i < str.length;i++){
letter[str.charAt(i)-'a']; //letter[str.charAt(i)-'A'] 大小写字母
}
}
字符串比较
切记使用equal方法去比较是否相等，直接==比较的是对象，不是字符串内容；
Character 数组转String
Arrays.stream(charArray).map(String::valueOf).collect(Collectors.joining());
字符串匹配操作
异位单词匹配
所谓异位单词匹配，就是单词字母相同，但顺序不一定相同，比如 cat tac;而cat 与 cat也是异位单词。
- 一般题目如果有限定小写字母，可以考虑int[26]来存储和计算。通过两个int[26]进行存储，可以在O(26)时间复杂度判断两个字符串是否是异位字符串。
子串匹配
- kmp算法
- 前缀树
KMP算法
什么是KMP算法？ KMP算法可以在O(m+n)的时间复杂度上完成字符串的匹配；字符串匹配就是给定一个主串T，和一个模式串S，判断S是否为T中的子串。
这个算法总结下来有两个关键的知识点：
- 字符串的前后缀
- 模式串的next数组
字符串的前后缀主要是用来理解该算法的原理，而next数组则是用于具体代码实现；
KMP算法的前后缀理解
在理解KMP算法之前，我们先简单的回顾一下传统的暴力匹配算法的步骤
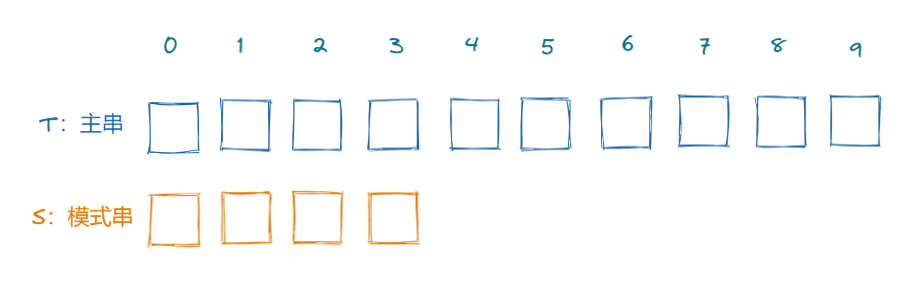我们从0位置开始，依次比较T和S中的字符是否相等，如果相等，则不断往后比较，如果不相等，
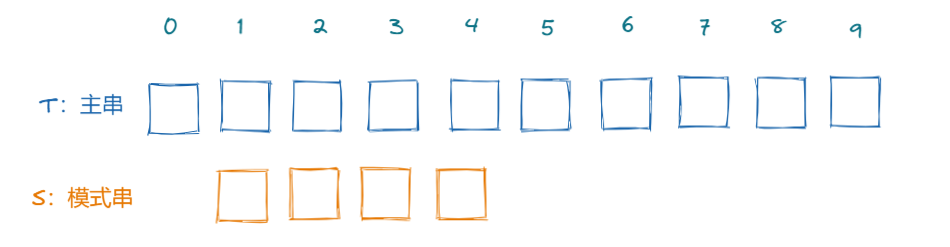S指针退回到0，T的指针指向当前头部的下一个位置。
这种做法很容易理解，时间复杂度最好情况的平均值为O(m+n)，最坏为O(m*n);
在暴力解法的过程中，只要遇到不相等的字符，不论如何S串指针都会回溯，T指针都会指向原来头部的下一个位置。但是我们可以观察下图
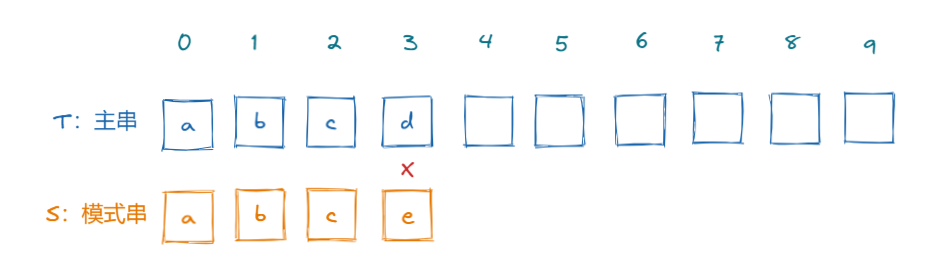此时匹配到下标为3的位置，发现字符不同了，我们要进行回溯，但此时我们观察模式串3位置之前的字符abc，可以很直观的发现，后面回溯的过程中，会不停的失败，因为a与bc都不相等。（在这个过程中，并不需要观察主串，因为T0~T2 = S0~S2）
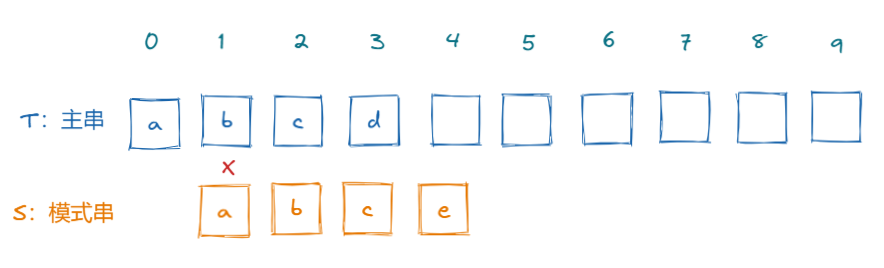
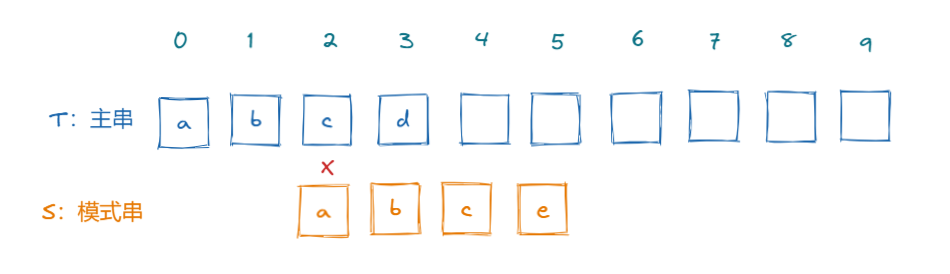这样的话，我们可以先得出一个简单的结论，如果在匹配的过程中，发现字符匹配失败了，则主串指针不变，模式串指针回到0，然后再重新开始匹配；
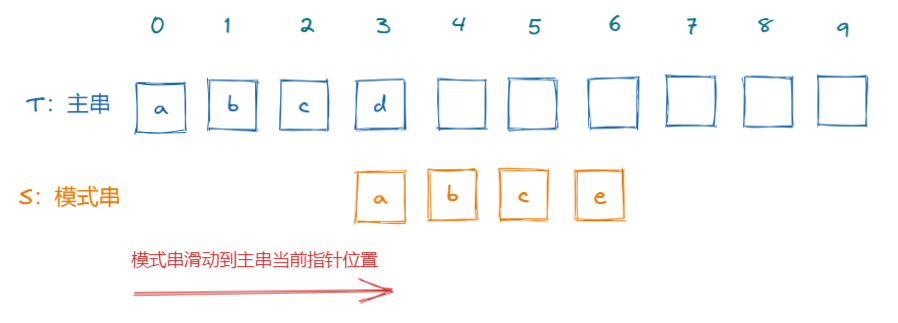
这个粗暴的结论很明显是错误的，如果模式串指针直接回到0，那么可能会错过正确开始匹配的位置；但是通过上面的结论，至少我们可以知道一点，那就是当发现字符不匹配的时候，我们主串的指针可以不需要回溯，只需要模式串向右滑动位置即可。
我们的模式串要右滑到哪个位置才合适呢？
我们可以假设需要右滑S[k]字符到位置J(k<j),
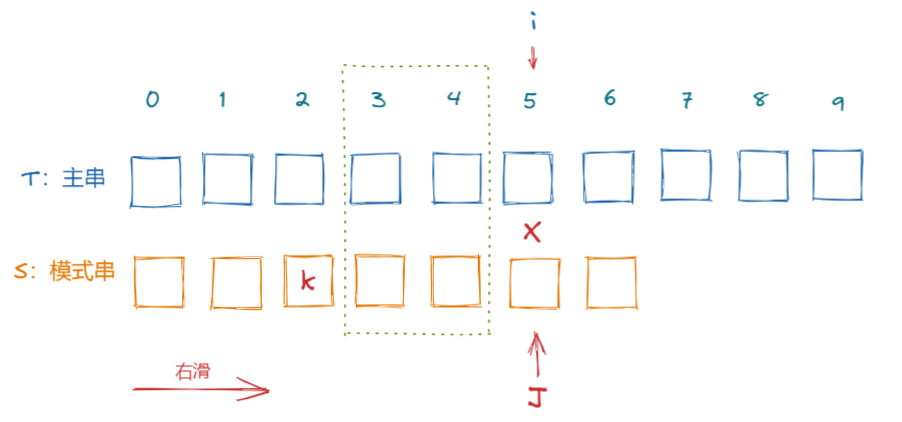
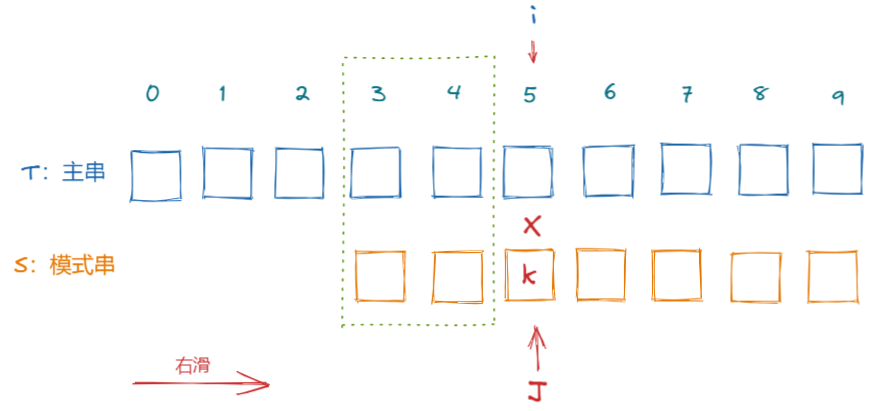此时有以下关系式
S0 ~ Sk-1 = Ti-k ~ Ti-1
而由于J位置前面已经是部分匹配了，所以有
Sj-k ~ Sj-1 = Ti-k ~ Ti-1
从而有
S0 ~ Sk-1 = S j-k ~ Sj-1
我们可以观察上面的图片，在移动前S[J]前面的部分已经匹配成功了，而我们将K位置移动到J，那么S0 S1 就是与T3 T4相等的，而移动前T3与T4又与S3 S4相等，从而有S0 S1 和S3 S4相等。
所以从这个关系式我们可以得出，向右滑动到k的这个位置，需要满足
S[0] ~ S[k-1] = S[j-k] ~ S[j-1]
而 S[0] ~ S[k-1] 和 S[j-k] ~ S[j-1]就是S[J]位置前面子串的最长前缀和后缀；
而我们的K位置，就是找到子串中最长相等的前缀和后缀后，最长前缀的下一个位置。
所以在KMP算法中，主串的指针位置不需要回溯动，我们也不许过多的关心它，我们只要知道，每次模式串S[J]和主串T[i]匹配失败后，我们需要找到S[j]前面子串最长相等前缀的下一个位置K，把他移动到J位置,在继续进行匹配，重复上述步骤，直到匹配成功或失败。
next数组
在前面了解了S[J]前面的最长相等前缀和后缀的概念后，并且知道了K的值为最长前缀的后一个位置。那么我们在进行匹配的时候，模式串的每一个位置都可能失败，那么失败后，每个位置要将前面的哪个位置K移动到当前位置呢？
通过前面的分析，我们知道了对于每个位置J，需要找到最长相等前后缀，然后最长前缀的下一个位置就是目标K;
那么在具体实现中，我们可以通过一个数组next[]来进行记录，从而有next[j] = k;并且要在开始匹配之前就求得这个数字。
那么问题来了，这个数组具体怎么实现呢？
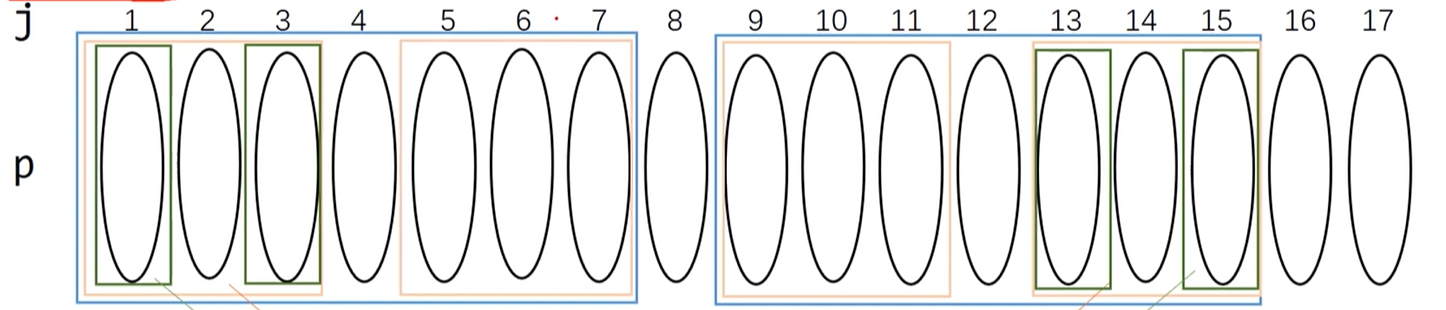
我们直接看这个图，假设我们要求next[17]的K值，我们要求得前面的最长前缀，我们可以通过next[16]来求
next[16]=8,那么1 ~ 7和9 ~ 15是相同的字符串（前后缀），此时如果8和16相同，那么next[17]=next[16]+1，也就是9，因为8，16相同，所以1 ~ 8 与 9 ~ 16相同，17的最长前缀为1 ~ 8 所以k就为 9；
那如果8 与 16不同，那我们需要求得next[8]的k值，假设是4，那么就有1 ~ 3 = 5 ~ 7 而 1 ~ 7 = 9 ~ 15 从而得到 1 ~ 3 与 13 ~ 15 此时在判断4 是否与16相等，相等则next[17] = next[8]+1;也就是4；
依次类推，直到求next1 ，因为第一个元素是没有前后缀的，所以此时next[17] = 1,表示移动到第一个位置
代码的写法：
int[] next = new int[s];
int j = 0 ;
int k = -1;//数组从0开始，所以用-1表示第一位的k值
next[j] = k;
while(j < s.length()-1){
//如果k为-1，则next[j+1] = 0
//相等，则next[j+1] = k+1;
if (k == -1 || needle.charAt(j) == needle.charAt(k)){
j++;
k++;
next[j] = k;
}else{
//否则，继续向前找最长前缀
k = next[k];
}
}
代码实现
public int matchString(String t,String s){
if (s.length() == 0){
return 0;
}
//构造next数组
int[] next = new int[s.length()];
int j = 0;
int k = -1;//数组从0开始，所以用-1表示第一位的k值
next[j] = k;
while (j < s.length()-1){
//如果k为-1，则next[j+1] = 0
//相等，则next[j+1] = k+1;
if (k == -1 || s.charAt(j) == s.charAt(k)){
j++;
k++;
next[j] = k;
}else {
//否则，继续向前找最长前缀
k = next[k];
}
}
int i = 0;
j = 0;
//两个指针j i 从0开始匹配
while (i < t.length() && j < s.length()){
//如果j=-1,即表示s串第一个就不相等，此时ij都向后移动
//相等则继续向后移动进行匹配
if (j == -1 || t.charAt(i) == s.charAt(j)){
j++;
i++;
}else {
//不匹配，模式串滑动，取出next[j]
j = next[j];
}
}
if (j >= s.length()) {
return i-s.length();
}
return -1;
}
前缀树(Trie)
前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。
Trie树优点是最大限度地减少无谓的字符串比较，查询效率比较高。核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
下面的代码，适用场景仅为字符串都是小写字母;
Trie中有两个属性，一个是children，表示字节点的同时，也表示子节点的值，因为是小写字母，所以下标也就代表了对应的字母；
所以其实按照树的结构来看，每个节点的值，其实反而是存在其父节点上的。而对于尾部节点，自然其chilren的值就都为null;
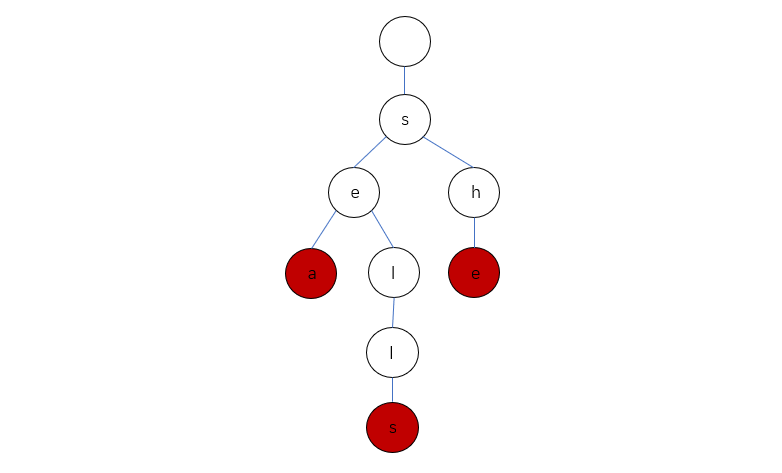
插入搜索都和链表的思路相似，插入就是取出字符串中的每个字符，然后逐一取node.children[char-‘a’] = new Trie();
搜索就是 node = node.children[char-‘a’];如果包含前缀或者指定的字符串，那么node最终不会为null，并且如果isEnd为true，表示搜索得到指定字符串。
class Trie {
//子节点，用数组存储，下标表示字母
private Trie[] children;
private boolean isEnd;
/** Initialize your data structure here. */
public Trie() {
children = new Trie[26];
isEnd = false;
}
/** Inserts a word into the trie. */
public void insert(String word) {
Trie node = this;
for(int i = 0 ; i < word.length();i++){
char ch = word.charAt(i);
int index = ch-'a';
if (node.children[index] == null){
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true;
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
Trie node = searchPrefix(word);
return node != null && node.isEnd;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;
}
private Trie searchPrefix(String prefix){
Trie node = this;
for(int i = 0 ; i < prefix.length();i++){
int index = prefix.charAt(i)-'a';
if (node.children[index] == null){
return null;
}
node = node.children[index];
}
return node;
}
}
回文
中心拓展算法
当我们需要判断一个字符串中的子串是否有回文时，可以用中心拓展算法；中心拓展算法的主要思路就是选取所有可能的回文中心点，然后左右同时拓展，如果存在左右值相等则继续扩展，否则就结束拓展；
中心拓展算法思路不难理解，唯一的问题是回文串是奇数还是偶数的问题。当回文串是奇数时，回文中心为单个字符，偶数时，中心为两个字符，所以我们寻求的回文中心要包含一个字符的情况，也要包含两个字符的情况。
假设我们的原字符串长度为n=4；
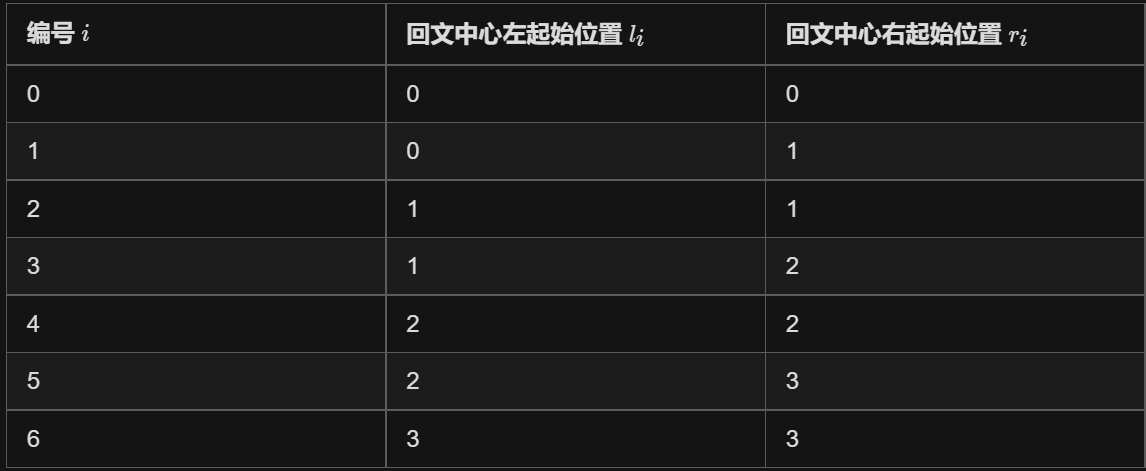通过上图可以知道，我们要遍历得到所有可能的回文中心。由此可得回文中心的数量为==2*n-1==;
并且对于每一个回文中心，他的左边界初始为 L = i/2 右边界为 R = i/2 + i%2;
通过该方式可以完整遍历一遍该字符，并且查询到该字符串中所有可能为回文的子串;不过时间复杂为O(n^2^);
马拉车算法
马拉车算法的基本思路，其实是建立在中心拓展算法上的，是对中心拓展算法的一种优化。我们先来分析中心拓展算法有什么不足的地方
- 回文子串长度可能是奇数的也可能是偶数的，这就导致我们选取回文中心的时候必须考虑选取一个回文中心和两个回文中心的情况
- 每次选取一个回文中心，都要从该中心向外扩散，有没有办法优化这一部分？
马拉车算法总结下来，就是对上面两个问题的优化
首先第一个问题，使用了一个很巧妙的方法，那就是在每个字符中间插入’#’字符，然后首尾在插入# 使其总得字符个数变为 2 * n + 1 ,也就是一定是奇数个，包括回文的子串，也都变为奇数个，而这就很方便我们进行回文中心的遍历，而且也不影响原串的回文特性,直接选取每一个字符作为回文中心即可，不用再考虑选取一个和两个字符作为回文中心的情况。
acadedaca
=> #a#c#a#d#e#d#a#c#a#
第一个问题解决了，我们来看第二个问题，每取一个中心就要向两边拓展，从而导致时间复杂度为O(n2^2);
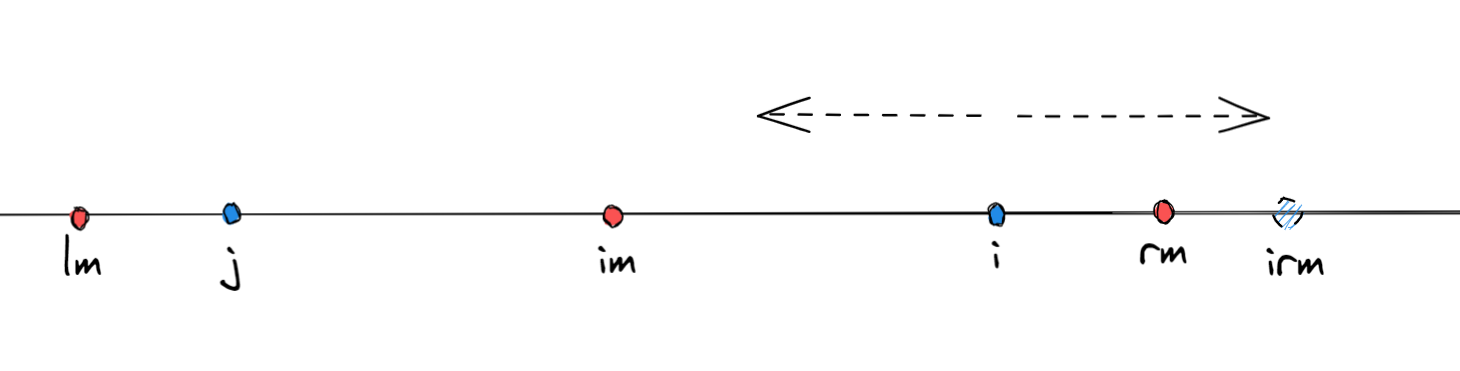
这个时候我们先来观察一个特性，那就是对于一个字符串中的某个回文子串，假设该回文子串的回文中心点为im,而他的回文半径长度为r(回文半径包括中心点自己),回文右端点位置位rm ,其中rm = im+r-1;同理，左端点为lm = i - rm + 1;
此时，假设我们在上面的条件下，要求im右边半径内的某个回文中心他的回文半径是多少(如果i不是回文串，回文中心本身也可以构成回文串，只不过此时回文长度为1)
按中心扩展算法，那就是直接从该点开始，双指针不断比较。但是我们观察到i是处于im的回文串中，所以i肯定有一个与之对称的位置 j ==( j = 2 * im - i)== 位于im的左边，并且j位置两变的字符与i位置两把的字符也都是对应的，那也就是说，==j在im回文串范围内，j的回文长度是可以对应到i的==。如下图
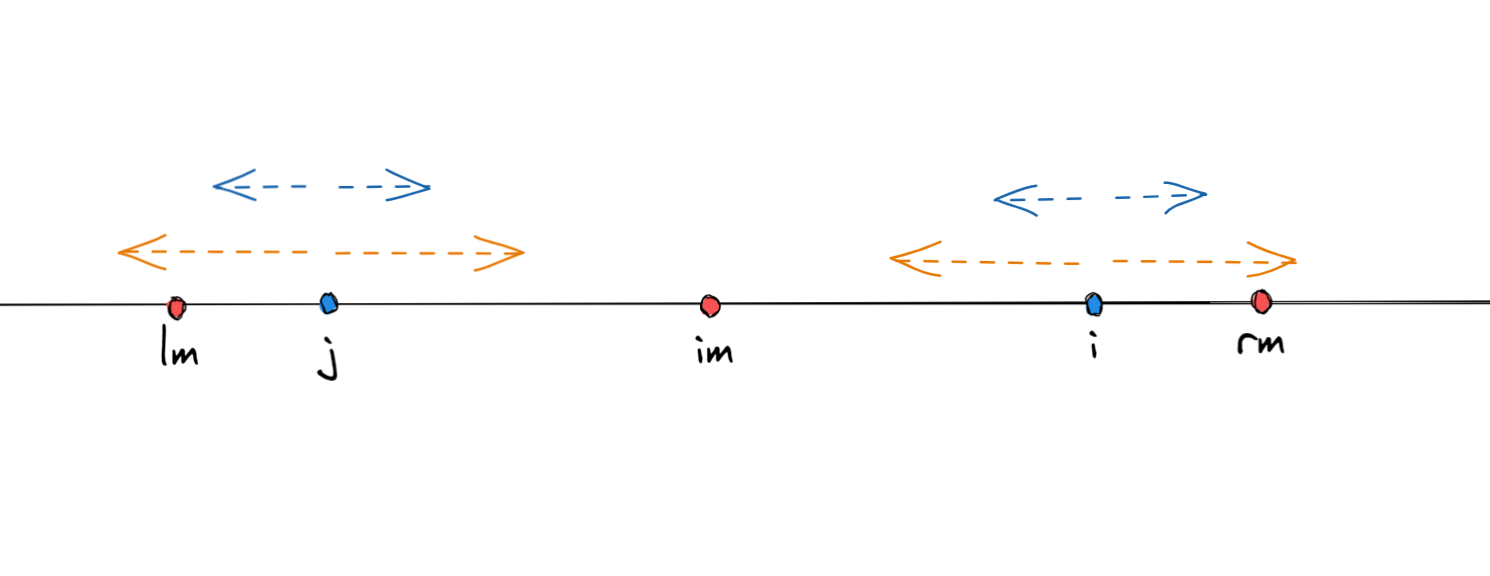
我们可以看到，j的回文长度其实分为两种可能
- j的回文范围在im的回文串范围内
- j的回文范围在im的回文串范围外（含边界）
如果在范围内，那很好理解，我们通过这个就可以知道i的回文范围就是跟j一样的，因为他们都是im的回文串，所以i的回文长度就等于j的回文长度。
如果在范围外，那也就是说，j的回文范围，超过了im的回文的边界，但是我们可以确定的是，在im的回文范围内的这部分，i和j也是对应的，也就是说i至少拥有从i到rm这部分的回文半径，确定了这部分后，在继续向外拓展比较，求得i的实际回文长度。
==这样对于每一个回文中心i，我们可以首先判断他是否处于某个回文串中，如果是，那么他就可以通过该回文串找到与之对应的j，通过该j可以确定i至少拥有的回文长度，然后在进行扩展.==
那么我们可以建立一个整型数组b[], ==b[i]就表示以i为回文中心的回文半径长度==，==rm==就表示当前最远的回文串右边界，==im==就是rm对应的回文中心。
初始rm,im都是0，我们遍历字符串，对于每一个i，我们执行以下操作
初始化
先判断i是否在im的回文串中
i > rm: 不在，初始半径长度就是1i <= rm: 求得b[i] = min(b[2 * im -i],rm-i+1)这就是前面讨论的j的回文半径在im的范围内还是范围外，这里体现出来的就是取 求b[j]的回文半径 和 rm到i的距离 的最小值。
扩散
初始化完毕之后就进行扩散，即不断比较 ==i+b[i]== 与 ==i-b[i]== 位置的字符是否相等，相等就b[i]++，即半径长度+1；
更新rm,im
在求得b[i]之后，要判断此时b[i]+i-1是否大于rm，是的话就要更新im为当前i，rm为b[i]+i-1。
关于rm的理解，因为我们要利用i前面的回文串，来快速初始化b[i]，相当于是通过前面的状态来加速i的扩散，所以我们要确保i处于某个回文串中。而i是不断从左往右遍历的，所以rm也需要不断的往右边更新。
我们看两个极端情况，比如字符串abcdefedcba。
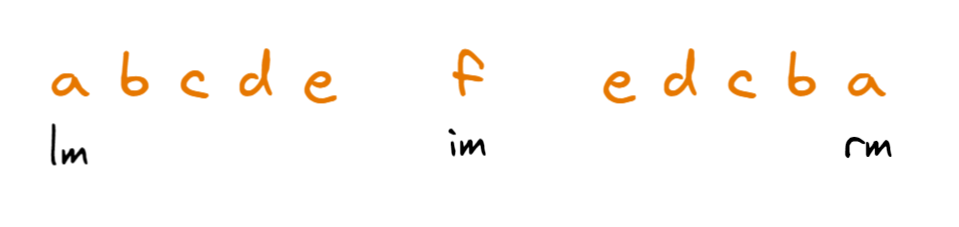
在im处于f的位置时，此时lm和rm正好就处于串的边界了，这个时候在遍历f右边的字符串，由于都处于f的回文中，所以都可以在O(1)的时间复杂度内确认b[i]，整个串遍历完也就花费n+n/2，时间复杂度为O(n)
另一种极端情况其实也是上面那串的子串 比如edcba,此时rm一直随着i不断往右边移动，知道结束，整个的花费也是O(n)
那么对于一般的情况，i如果在范围内，O(1)就确定了他的b[i]，如果超过范围，那么就会从rm开始进行扩散，扩散结束后会更新rm，对于下一个i重复上述判断，这样就会造成两个操作，要么o(1)确定b[i]，要么不断的推进rm,直到rm到达串尾。而这也是整个马拉车算法之所以时间复杂度为O(n)的原因。
模板代码
关键就是求出b[i] 表示以i为回文中心的最大回文半径。
开头加一个 $，并在结尾加一个 !，这样开头和结尾的两个字符一定不相等，循环就可以在这里终止，不需要额外判断边界。
public void manacher(String s) {
StringBuilder sb = new StringBuilder();
sb.append("$#");
for(char sc:s.toCharArray()){
sb.append(sc);
sb.append('#');
}
int n = sb.length();
sb.append('!');
String t = sb.toString();
int[] b = new int[n];
//rm 为当前最远的回文右端点，im为其对应的回文中心。
int im = 0,rm = 0;
for(int i = 1 ; i < n;i++){
//当前i是否在rm内，是的话b[i] = Math.min(b[2*im-i],rm-i+1) 否则 = 1；
b[i] = i <= rm ? Math.min(b[2*im-i],rm-i+1):1;
while (t.charAt(i+b[i]) == t.charAt(i-b[i])){ //初始后的回文范围为 i-b[i]+1 ~ i+b[i]-1;
b[i]++;//左右相等，半径+1
}
//当前i的半径加上i的位置，比rm的位置还靠右，则更新rm和im
if (i+b[i]-1 > rm){
im = i;
rm = i+b[i]-1;
}
}
return ans;
}
