背包问题 - CHuiL

01背包问题

当前有n件物品，每件物品都价值v，和重量w两个属性；我们手上还有一个背包，设背包最大所能容纳的重量为C。求如何拿取物品才能使在有限容量的背包中所获得的价值最大。

解体思路

使用动态规划来解决这一问题，当我们来到第i件物品时，我们的包里还有容量c，我们希望选择的结果能使价值最大，所以我们可以设B(i,c)表示在面临第i件物品时，包里容量还有c的情况下的所能拿取的最大值。
例如我们有1，2，3，4，5 一共五件物品，总容量为C；那么B(5,20)表示面临第5件物品时，且容量为20的最大值价值，也即最终的最大价值。而在面临第5件物品时，有三种选择情况

容量足够，拿取第5件物品；则B(5,20) = B(4,20-w5)+v5;即拿取第五件物品之后，接下来面对的就是后面的物品。B(4,20-w5)就是用剩余的容量拿取后面的物品所能得到的最大价值。
容量足够，不拿取第五件物品;则B(5,20) = B(4,20);同理，用容量20去拿取后面的物品所获得的最大值。
容量不足，不拿取;B(4,20);

所以我们可以总结出以下公式

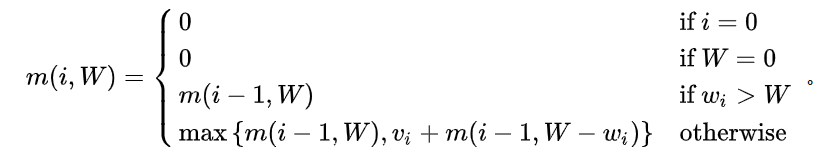
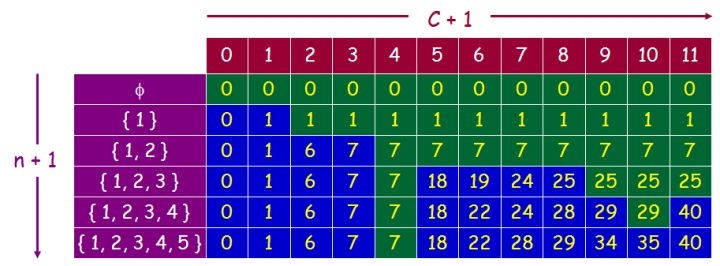
构建dp二维表来存储

每一行代表所能选择到的所有物品，每一列代表当前总容量（0~C）。

type Element struct {
	w int
	v int
}

func Knapsack10(elemt []Element, C int)int{
	N := len(elemt)

	DP := make([][]int,N+1,N+1)
	for i,_ := range DP{
		DP[i] = make([]int,C+1)
	}

	for i:=1;i<=N;i++{
		for c:=0;c<=C;c++{
			if elemt[i-1].w>c{
				DP[i][c] = DP[i-1][c]
			}else{
				DP[i][c] = Max(DP[i-1][c],DP[i-1][c-elemt[i-1].w]+elemt[i-1].v)
			}
		}
	}

	fmt.Println(DP[N][C])
	return DP[N][C]
}

将二维的数组转换为一维数组

将原来的容量的遍历顺序逆序，这样便可以保证dp[c-w]代表的是dp[i-1][c-w]了。即也保证了物品只能选择一次；而且遍历容量的时候，重量为v的物品不会影响0~v之间的状态。

type Element struct {
	W int
	v int
}


func Knapsack10(elemt []Element, C int)int{
	N := len(elemt)

	DP := make([]int,C+1)

	for i:=1;i<=N;i++{
		for c:=C;c>=elemt[i-1].W;c--{
			if elemt[i-1].W>c{
				DP[c] = DP[c]
			}else{
				DP[c] = Max(DP[c],DP[c-elemt[i-1].W]+elemt[i-1].v)
			}
		}
	}

	fmt.Println(DP[C])
	return DP[C]
}

完全背包问题

大致与01背包相同，只是一件物品可以选择无限次例如

背包总容量：6
重量 价值
 1   1
 2   3
 3   4
 4   5

输出：9
即拿了三件重量为2，价值为3的物品

这里我们面临的选择除了拿和不拿之外，还有能拿几件的问题；W为总容量；则有

dp[i][w] = dp[i-1][w] { 0<=v<wi }
dp[i][w] = max(dp[i-1][w],dp[i][v-wi]+vi) { wi<=w<=W }

同样是使用二维表格来求解

以输入第一，二个物品为例

输入第一个
f[1][0]=f[0][0]
f[1][1]=max(f[0][1],f[1][1-1]+1)
f[1][2]=max(f[0][2],f[1][2-1]+1)
f[1][3]=max(f[0][3],f[1][3-1]+1)
f[1][4]=max(f[0][4],f[1][4-1]+1)
f[1][5]=max(f[0][5],f[1][5-1]+1)
f[1][6]=max(f[0][6],f[1][6-1]+1)

输入第二个
f[2][0]=f[1][0]
f[2][1]=f[1][1]
f[2][2]=max(f[1][2],f[1][2-2]+3)
f[2][3]=max(f[1][3],f[1][3-2]+3)
f[2][4]=max(f[1][4],f[1][4-2]+3)
f[2][5]=max(f[1][5],f[1][5-2]+3)
f[2][6]=max(f[1][5],f[1][6-2]+3)

得到如下表

|-|0|1|2|3|4|5|6| —|—|—|—|—|—|—|—| 0|0|0|0|0|0|0|0| 1|0|1|2|3|4|5|6| 2|0|1|3|4|6|7|9| 3|0|0|0|0|0|0|0| 4|0|0|0|0|0|0|0| …

所以有以下代码

for i:=1;i<=len(elemts);i++{
    for v:=0;v<=W;v++{
        if v>=elemts[i-1].w{
            dp[i][w] = max(dp[i-1][w],dp[i][v-elemts[i].w]+elemts[i].v)
        }else{
            dp[i][w] = dp[i-1][w]
        }
    }
}

return dp[len(elemts)][W]

优化为一维数组

01背包问题的时候就通过逆序遍历重量来使dp[c-w]能正确表示前一个状态（上一个物品的重量），而在这里不同的是，我们要获取的是当前状态（物品）的重量，或者说该物品前面已加入的重量；所以就可以从0开始遍历W，从而有

dp[c] = max(dp[c],dp[c-w]+v) //这里c>c-w,所以dp[c]还是表示的前一个物品的重量；

所以有以下代码

for i:=1;i<=len(elemts);i++{  //这里的两层for循环是可以颠倒的
    for v:=0;v<=W;v++{
        dp[v]=max(dp[v],dp[v-elemts[i].w]+elemts[i].v)
    }
}

return dp[len(elemts)][W]

leetcode上的类似题目

416. Partition Equal Subset Sum

大意就是给定一个整型数组，求该数组能否分为两个子数组，要求他们的和相等；
这道题之前就已经做过了，但是并没有做出来，也是看到别人的解法，看了好久勉强了别人的做法。
现在重新学了01背包问题，再去看这道题发现就是01背包的问题。。

这里转换一下，把每个值看成重量，问题就变成，能否从这堆物品中找出重量刚好为总重量的一半的物品；对于每一个物品，都有那或者不拿的选择，设有dp[i][w]表示共有i件物品，是否能凑齐重量刚好为w；那么dp[i][w] = dp[i-1][w]||dp[i-1][w-nums[i]]
不拿就看后面的能否凑够w，拿了就看后面的能否凑够w-nums[i]；是不是就是01背包问题，构造相同的二维表，只是不在是表示价值，而单纯只是一个true false而已；这样去想这道题就容易很多，之前借鉴的解法看了半天才理解，理解之后就马上忘记了。

func canPartition(nums []int) bool {
    sum:=0
    for _,n:=range nums{
        sum+=n
    }
    if sum&1==1{
        return false
    }
    
    target := sum>>1
    
    dp := make([]bool,target+1)
    dp[0]=true
    for _,num:=range nums{
        for i:=target;i>=num;i--{
            dp[i] = dp[i]||dp[i-num]
        }
    }
    
    return dp[target]
    

474. Ones and Zeroes

In the computer world, use restricted resource you have to generate maximum benefit is what we always want to pursue.

For now, suppose you are a dominator of m 0s and n 1s respectively. On the other hand, there is an array with strings consisting of only 0s and 1s.

Now your task is to find the maximum number of strings that you can form with given m 0s and n 1s. Each 0 and 1 can be used at most once.

大意就是，m，n分别代表0 和 1的个数，在给你个字符串数组，每个字符由01构成，问从这个数组中找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。

例子

Input: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
Output: 4

Explanation: This are totally 4 strings can be formed by the using of 5 0s and 3 1s, which are “10,”0001”,”1”,”0”

这道题也是01背包问题，只是价值重量转化为0 1 的个数而已,同样可以得到类似的状态转化方程 dp[i][m][n] = max(dp[i-1][m][n],dp[i-1][m-Mi][n-Ni]+1
在熟悉了上面的解法，这个方程也不难理解了，就是在对第i个字符时，有选择拿去它或者不拿取它，不拿去则最大数量由后面字符的决定，拿去了则将M，N的个数对应的减少，总量+1；同样是构造二维表
这里的二维表中，可以看成i,(m,n)的形式；

代码如下

func findMaxForm(strs []string, m int, n int) int {
	dp := make([][]int,m+1)
	for i,_:=range dp{
		dp[i] = make([]int,n+1)
	}

	for _,s := range strs{
		count0 := strings.Count(s, "0")
		count1 := len(s) - count0

		if count0>m || count1 > n{
			continue
		}

		for M:=m;M>=count0;M--{
			for N:=n;N>=count1;N--{
				dp[M][N] = max(dp[M][N],dp[M-count0][N-count1]+1)
			}
		}
	}
	return dp[m][n]
}

322. Coin Change

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

例子

Input: coins = [1, 2, 5], amount = 11
Output: 3 
Explanation: 11 = 5 + 5 + 1

这道题就是完全背包问题了，所以我们可以有一个二位dp数组 dp[i][v] = min(dp[i-1][v],dp[i][v-coins[i-1]]+1)
这里需要注意的就是题目要求的是求最小值，所以dp[0][0]=0 dp[0][1…amount]要取amount+1,即最大值；二维数组的代码

func coinChange(coins []int, amount int) int {
    dp := make([][]int,len(coins)+1)
    
    for i,_ := range dp{
        dp[i] = make([]int,amount+1)
    }
    
    for v:=1;v<=amount;v++{
        dp[0][v] = amount+1
    }
    
    dp[0][0] = 0
    
    for i:=1;i<=len(coins);i++{
        for v:=0;v<=amount;v++{
            if v>=coins[i-1]{
                dp[i][v] = min(dp[i-1][v],dp[i][v-coins[i-1]]+1)
            }else{
                dp[i][v] = dp[i-1][v]
            }
        }
    }
    
    res :=  dp[len(coins)][amount]
    if res>=amount+1{
        return -1
    }else{
        return res
    }
}

同样的，这里也可以转换为一维数组，思路是一样的

func coinChange(coins []int, amount int) int {
    dp := make([]int,amount+1)
    
    for v:=1;v<=amount;v++{
        dp[v] = amount+1
    }
    
    for _,coin := range coins{
        if coin<=amount{
            dp[coin] = 1
        }
    }
    
    for _,coin := range coins{
        for v:=0;v<=amount;v++{
            if v>=coin{
                dp[v] = min(dp[v],dp[v-coin]+1)
            }
        }
    }
    
    if dp[amount]>=amount+1{
        return -1
    }else{
        return dp[amount]
    }
}

494. Target Sum

You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

大意就是给你一个正整数数组，对每一个值可以选择+，-号，求选择+-号后所求得的和为目标S的方法数

Input: nums is [1, 1, 1, 1, 1], S is 3. 
Output: 5
Explanation: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

There are 5 ways to assign symbols to make the sum of nums be target 3.

这道题其实也不难看出本质还是01背包问题，对每个值都有+-号的选择；其实按着这种思路可以写出下面的公式

dp[i][s] = dp[i-1][s-1]+dp[i-1][s+1]

上面的公式也好理解，如果我们给当前数值i选择+号，那么就求后面的元素和为s-1，如果选择-号，后面的元素和为s+1；这条公式起初看上去好像没什么问题（至少一开始真没看出问题 orz…），结果马上写完一跑就发现不对劲，这样写的话还得处理负数。比如当我现在在i=2，即当前有两个值1,1可以选择，那么dp[2][0] = dp[i][-1]+dp[i][2] 这就有点难搞了。

这里其实还可以有另外一个很巧妙的方式

假设有
    S1+S2=SUM;
    S1-S2=tar;
则有
    S1=(SUM+tar)/2 

所以问题就转化为了求数组和为S1的方法数，且SUM和tar都是已知值；

代码如下

func findTargetSumWays(nums []int, S int) int {
    sum := 0
    for _,num := range nums{
        sum+=num
    }
    
    if (sum+S)&1==1 || sum<S {
        return 0
    }
    
    tar := (sum+S)/2
    dp := make([]int,tar+1)

    //这里为dp[0][0]=1；元素值为0，目标值为0，那么方法数为1，不然后面的会无法叠加
    dp[0] = 1 
    for _,num := range nums{
        for i:=tar;i>=num;i--{
            dp[i] = dp[i]+dp[i-num]   
        }
    }
    
    return dp[tar]
}