旅行商问题

#问题描述 要求旅者从一座城市出发，路过所有城市一次且仅有一次，最后回到出发点所花费的最小路径成本。

#动态规划解法 动态规划就是要将问题分解为更小的问题，然后由每个小问题的最优解来求出最终的结果。 假设我们的起点为s，最终肯定存在这么一条最短路径s,s1,s2,s3…sn,s；因为已经是最短路径了，所以当我们从s1开始出发在回到s，即s1,s2,s3…sn,s也同样是最短路径。同理一直到sn出发到s。此时从sn出发回到s的最短路径花费就为Sn到s的路费。 所以我们从s出发时，设所有未经过的点集合为V,设d(s,V)表示从s出发，经过V中所有点一次最终回到s的最小花费。 那么进一步缩小问题，即存在一个$S_1$，使得S到$S_1$在最短路径上，那么就有$d(S_1,V-S_1)$,表示从S1出发，进过所有未经过的点在回到S的最少花费。一直缩小直到最后d(Sn,{})，表示从sn出发下一站即返回s。d(sn,{})=$C_{Sni}$;C表示两点之间的花费。

那么就可以求得其状态转化方程

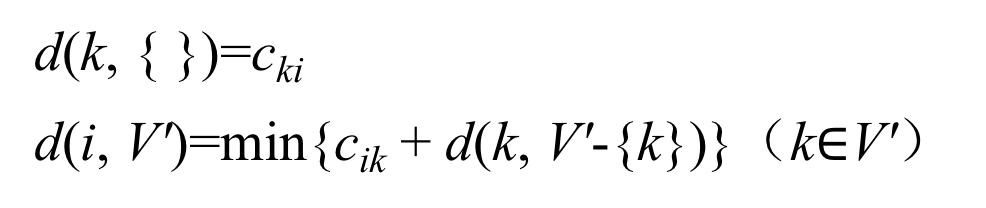
字节跳动-毕业旅行问题

小明目前在做一份毕业旅行的规划。打算从北京出发，分别去若干个城市，然后再回到北京，每个城市之间均乘坐高铁，且每个城市只去一次。由于经费有限，希望能够通过合理的路线安排尽可能的省一些路上的花销。给定一组城市和每对城市之间的火车票的价钱，找到每个城市只访问一次并返回起点的最小车费花销。

输入描述:

城市个数n（1<n≤20，包括北京） 城市间的车票价钱 n行n列的矩阵 m[n][n]

输出描述:

最小车费花销 s

输入例子1:

4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0

输出例子

13

我们使用二进制来表示集合v，并且从上面的公式可以知道我们需要从集合开始遍历，并且为了不重复计算，我们从集合为0开始反过来计算，动态规划的问题经常都是从上往下去分析问题，从下往上去解决问题的；不过这里要注意的是，我们不是说从集合为0个，1个，两个这样去往回算，而是利用二进制的表示方法，让他从1~2^n-1遍历；

package main
import "fmt"
func main(){
    N := 0
	fmt.Scan(&N)
	city := make([][]int,N)
	for i,_:=range city{
		city[i] = make([]int,N)
	}

	for i:=0;i<N;i++{
		for j:=0;j<N;j++{
			fmt.Scan(&city[i][j])
		}
	}
	b := 1<<(uint(N)-1)
	dp := make([][]int,N)
	for i:=0;i<N;i++{
		dp[i] = make([]int,b)
	}

	for i:=0;i<N;i++{ //集合为0时，到达s0的票价就是该城市到s0的票价
		dp[i][0] = city[i][0]
	}

	for set:=1;set<b-1;set++{ //从1~b-1遍历
		for c := 1;c<N;c++{ //每个城市都要有对应的集合，不过该集合中不能保护c城市本身 
			if (1<<uint(c-1)&set)==1{
				continue
			}

			min := 99999
			for j:=1;j<N;j++{
				if (set&(1<<uint(j-1)))==0{ //选出该集合中的城市
					continue
				}
				tmp := city[c][j]+dp[j][set^(1<<uint(j-1))]
				if tmp<min{
					min = tmp
					dp[c][set] = tmp
				}
			}
		}
	}

    //前面已经求得的除s0外所有城市到达s0的最小路径了，接下来就是要从s0分别走其他城市的最小值
	min := 99999
	for i:=1;i<N;i++{
		tmp := dp[i][(b-1)^(1<<uint(i-1))]+city[0][i]
		if tmp<min{
			min = tmp
			dp[0][b-1]=tmp
		}
	}

	fmt.Println(dp[0][b-1])
}

• ← Previous Post
• Next Post →