应用场景
- c++中用来实现map和set的数据结构
- Java中实现HashMap，TreeMap
- Linux内核中完全公平调度器，大量实时计算程序
从2-3树查找树说起
2-3树指的是树的节点是由2-节点或3-节点组成的；所谓2-节点指的是该节点有1个值，两条链；3-节点就是有2个值，3条链； 如下图，3-节点中，两个值是左边小于右边，最左边的链接链的节点表示小于3-节点所有值得节点，中间链链接在两个值之间的节点， 最右边的链接链的是大于当前节点所有值得节点；
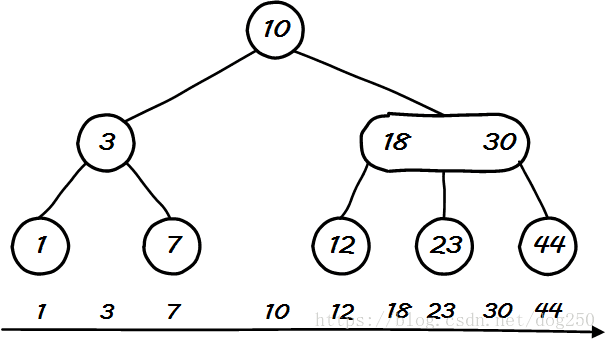
一颗完美平衡的2-3查找树中的所有空链（叶子节点下的nil节点）到根节点的距离是相同的；为了达到完美平衡，在插入的时候就要符合一定的插入规则
1.根据查找树的查找规则，找到要插入的位置，如果要插入的位置是一个2-节点，那么直接添加到该节点变成一个3-节点
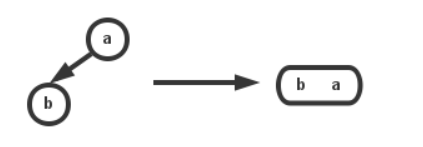
2.如果插入的节点是一个3-节点，那么此刻可以先将它加入到3-节点中，变成一个4-节点，不过我们并不需要4-节点，所以需要进行转换，可以将它转化成由3个2-节点组成的树；
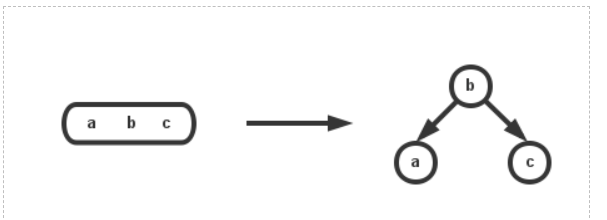
3.而在这里，我们为了平衡，是将中间的值（这里为b）向上移动到其父节点中；如果父节点为2-节点，那么就结束插入操作；如果父节点为3-节点，那么同理需要在转换，将其中间值在向上移动，直到根节点为4-节点时，继续相同的操作，将中间值往上提（实际上此时树的深度+1了）；
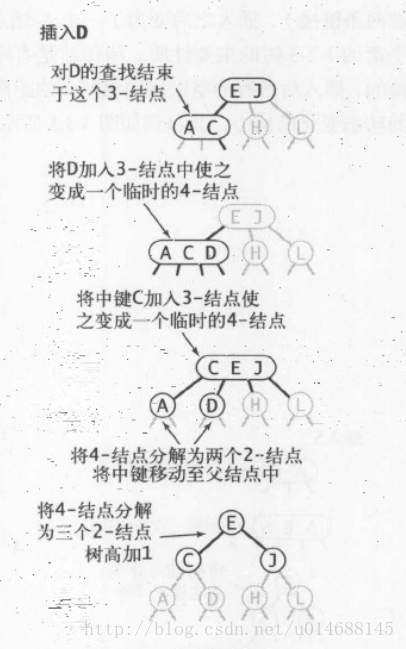
其实总结下来，就是插入的节点如果位置足够（2-节点），就让新节点插入当前节点构成3-节点，一旦构成4-节点了，就要将中间值向上移动，直到根节点； 这样的局部变换不会影响整颗树的有序性和平衡性，也就是说，这样的操作下来，整颗树都是完美平衡的；
红黑二叉查找树
按照2-3树理论上可以达到完美的平衡；但是真正实现起来却很困难，需要大量的代码而且产生的额外开销可能会使算法比标准的二叉查找树更慢；
而红黑二叉查找树就是一种表达并实现他的简单数据结构；它是标准的二叉查找树，即全部都是2-节点；
红黑节点
首先理解是什么红节点，黑节点，以及这里的红节点和2-3树中的节点是什么关系；
我们知道2-3树中有3-节点，而红黑二叉查找树全是2-节点，而这里是通过将两个节点（父节点和左子节点）用一条“红链接”连接起来，构成一个3-节点；
关于红黑链接的规矩
- 红链接必须均为左链接
- 没有任何一个节点同时可以和两条红链接相连
- 其他的普通的链接就是黑链接
- 每个节点都有一条指向自己的链接（父节点指向它），所以指向它的链接是什么颜色的，该节点就是什么颜色的；
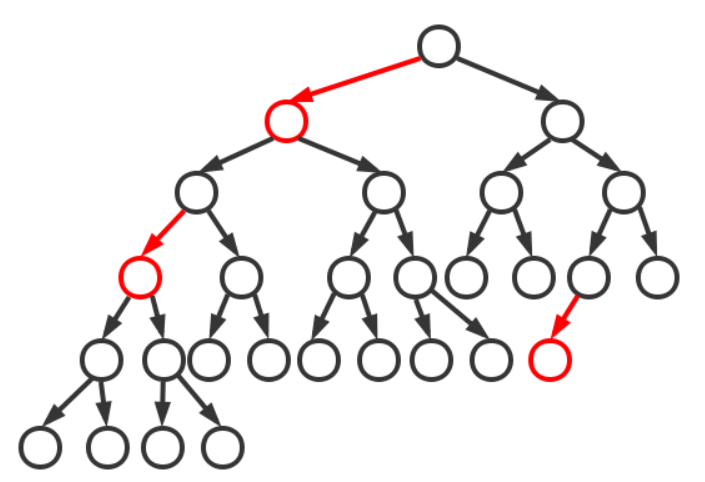
将这些红色的链接拉平，看起来就像一颗2-3树了
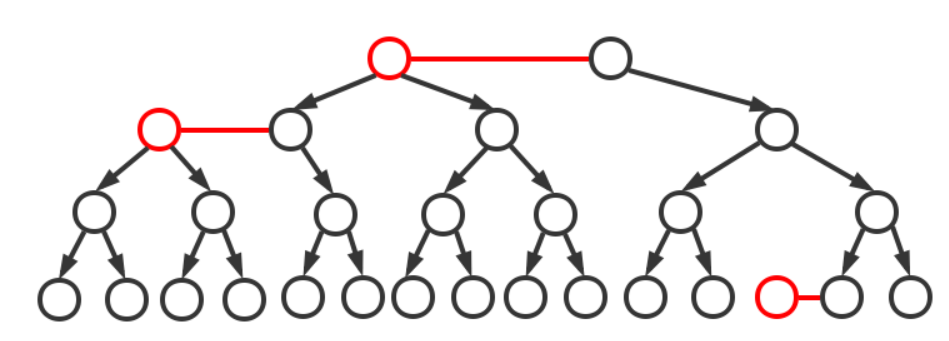
插入（插入的链接都为红色，即新节点都为红色节点）
如果树为空，那么直接插入的节点为根节点，颜色标为黑色；
新节点插入到父节点的右边
- 若父节点左子节点为黑色，则以父节点进行左旋转，将红色链接旋转到右边
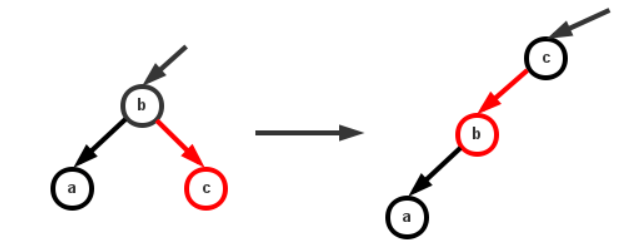
- 若父节点左子节点为红色，此时父节点左右子节点都为红色节点，则左右子节点置黑，父节点置红
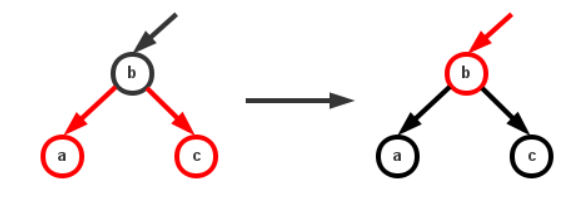
新节点插入到父节点的左边
- 若父节点为黑色节点，则不需要额外操作
- 若父节点为红色，此时需要以祖父节点为当前节点进行右旋转，旋转成左右红色节点的情况，然后进行颜色转换，左右子节点染黑，父节点染红；
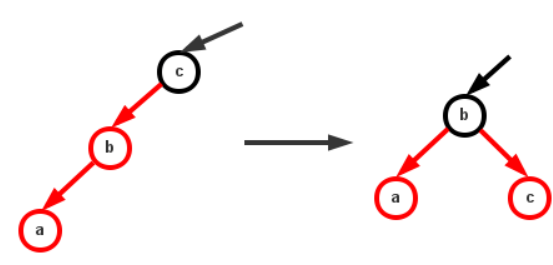
总的来说，插入就是将右边的红色链接或者是某个节点同时有两条红色链接的，对他进行旋转，旋转成左右红色节点的情况，然后再进行颜色转换， 将左右子节点染黑，父节点染红，然后以父节点为当前节点继续进行相同的判断，直到不破坏规则为止；最后若为根节点，则一起变黑；
这里说一下两条规则，为什么不能有右边的红链接以及不能有连续两条红色链接； 不能有两条红色链接就是为了消除4-节点，当他转化成左右红节点的形式时，在将中间的节点染黑，其实就是应对着2-3树中将4-节点的中间值移动到父节点之中； 不能有右链接，那是因为3-节点的形式就是这样的，左边的小于右边的，而小的那个就是父节点的左子结点；
删除
删除操作大致思路和二叉查找树的删除操作类似
- 如果是叶子节点，那么直接删除；
- 如果是非叶子节点，右边的最小值来替代当前节点（后继节点），右边最小（即变成了删除叶子节点）； 问题在于要寻找删除节点的过程。我们先看2-3树种的删除寻找过程
2-3树中的删除操作
而在2-3树中为了保持平衡，删除必须不能删2-节点，否则就不满足完美平衡的2-3查找树，所以在往下查找的时候要确保遍历的节点都不是2-节点，
即要搜寻到的位置要构成一个3-节点或者4-节点，这样删除的时候就可以从3-节点或者4-节点中删除而不影响平衡；有下面几种情况：
1.如果下一个节点不是2-节点，进入下一个节点；
2.如果下一个节点是2-节点，不过它的兄弟节点不是2节点，那么将它兄弟节点中的一个值移动到父节点中，然后父节点在移动一个值与它构成一个3节点
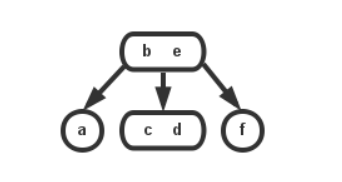
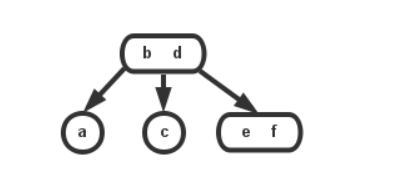
3、如果下一个节点是2-节点，且他的兄弟节点都是2-节点，那么从父节点中移动一个值，与它和它最靠近的兄弟节点构成一个4-节点；
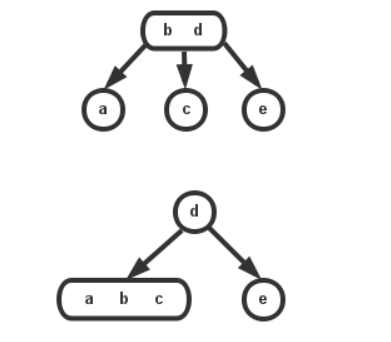
4、如果是在根节点，而且根是2-节点，左右子节点也都是2-节点，那么直接合并成一个3-节点；
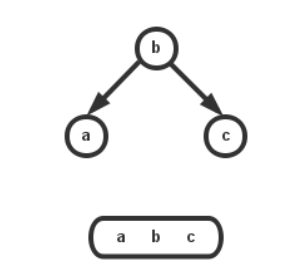
总结以上的情况，主要操作就是两个，优先从兄弟节点“转移”一个值来构成3-节点，没有再从父节点获取一个值来和兄弟节点构成4-节点；
红黑树中的删除操作
主要是以下操作：
1.若下一个节点为左节点，且不为红节点；直接“反色”，构成一个3节点
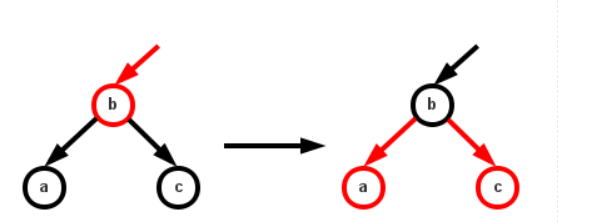类似的2-3树图如下
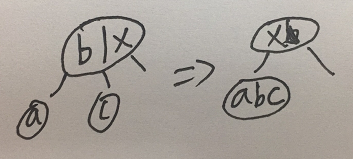
2.若下一个节点不为左子节点，则需要将父节点中要获取的值旋转至3-节点的结构，然后进行反色；
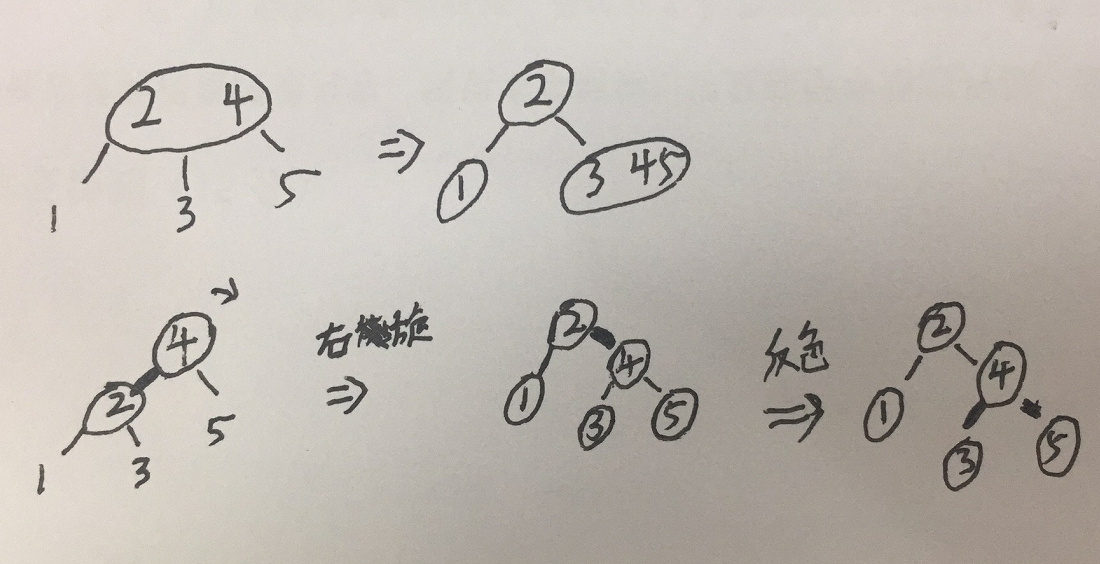
如上图，下一个节点为5或者3，那么都需要获取父节点的4，然后构成3-节点，为了构成3-节点，需要对4进行右旋转，然后进行反色；
3.从兄弟节点获取值，需要将兄弟节点的值旋上去父节点，然后再将父节点旋下去给子节点；
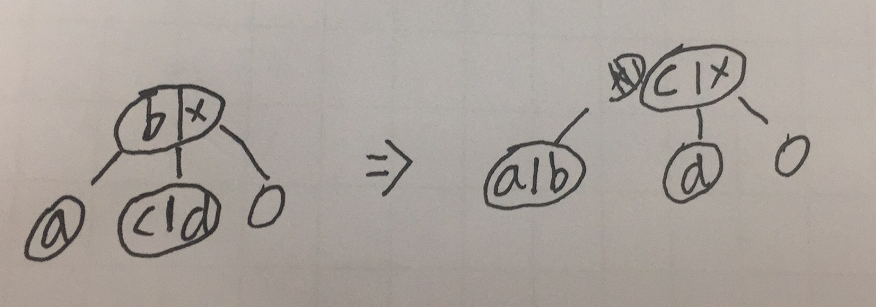
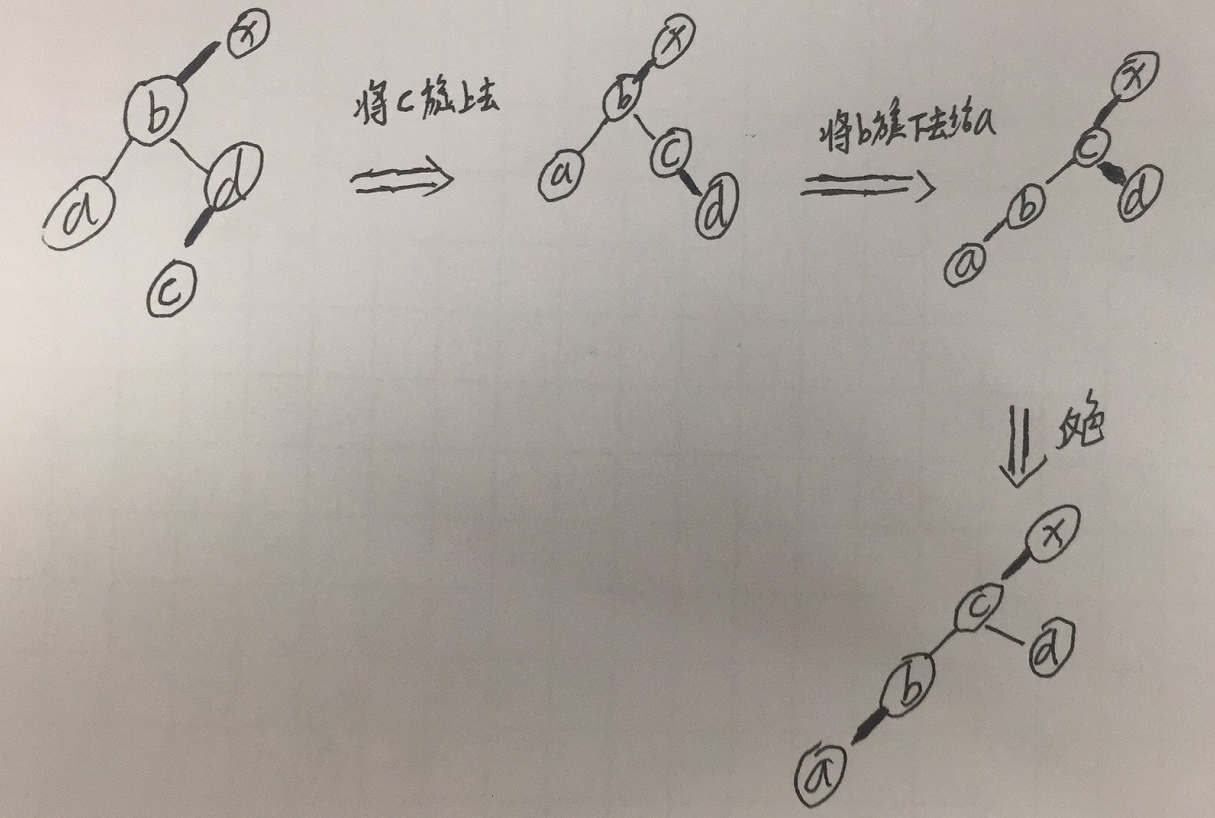
红黑树节点的删除
通过以上的变化，将2-节点转换成3-节点或者4-节点，然后在删除的时候，如果该节点为红节点，那么直接删除就好了。如果该节点为黑节点，那么他的左儿子一定是红节点，因为我们保证每个遍历到的节点都不是2-节点，所以他一定有左子红节点和它构成3-节点或者4-节点，所以将该左子节点旋上来，使要删除的节点变成红节点，然后再直接删除就好了；
