每个节点都有一个平衡因子BF：即该节点左右子树的高度差的绝对值
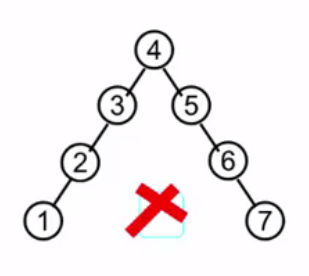
例如这里，对于节点4，他的平衡因子为0；但是对于节点3，他的平衡因子为2，因为左边高度为2，右边为0；
所以一颗搜索二叉树是否平衡，衡量的标准就是：对所有节点，BF<=1;
对于每插入一个新的节点，都要进行判断是否平衡，造成不平衡的情况有以下四种：
1.RR型破坏：
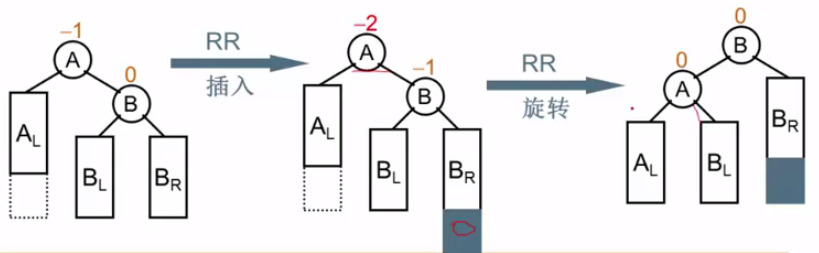新插入的节点使该树节点A不平衡，造成不平衡的位置位于A的右子树的右子树上，所以需要进行旋转（从方向上来看是进行逆时针旋转），就将值为中间的节（B）点拎上去,并调整子树的位置，最左最右保持不变，BL比B小，比A大，自然放到A的右边。具体如下：
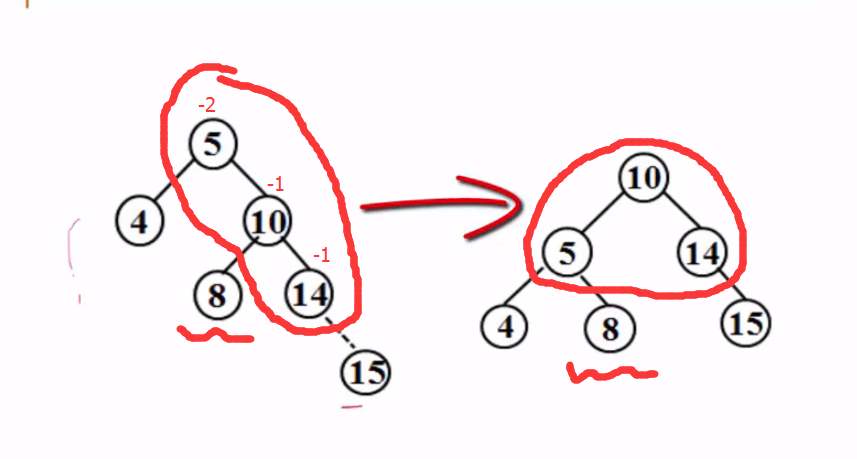旋转看关键的三个节点（5，10，14），将值为中间的节点拎上去，并将8的位置调整到5的右子树。
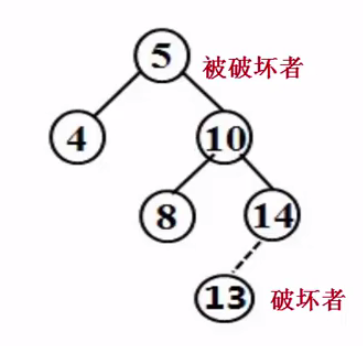
在看一种情况，此时在14这个节点的左边插入13,此时对于5来说，平衡破坏，而13这个破坏者位于5的右子树（10）的右子树（14）上，所以还是RR型，操作同上面一样。
2.LL型破坏：
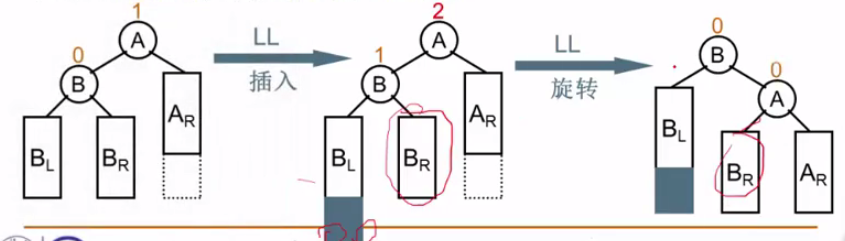
类似RR型，只是位置从右右变为左左，即插入的节点位于A的左子树的左子树上，所以此时要进行LL旋转（顺时针），最左最右边的子树不变，BR比A小，比B大，所以放入到A的左边子树上。
3.LR型破坏：
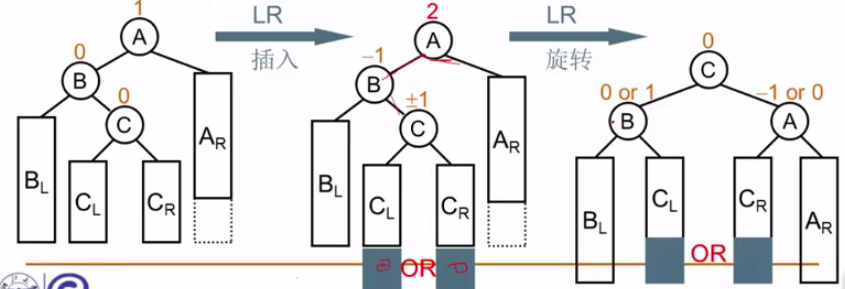
此时可以看到，新插入的节点位于C的下面（不管是左边还是右边），他为对于被破坏者A来说，都是位于左子树的右子树，所以是LR型，此时看关键的三个节点（ABC），因为旋转主要就是对他们三个进行旋转，同样是将中间值得节点拎上来，然后最左最右子树位置不变，调整CL,CR的位置，CL比C小，比B大，放在B地右边，CR比C大，比A小，放在A地左边。
具体例子：
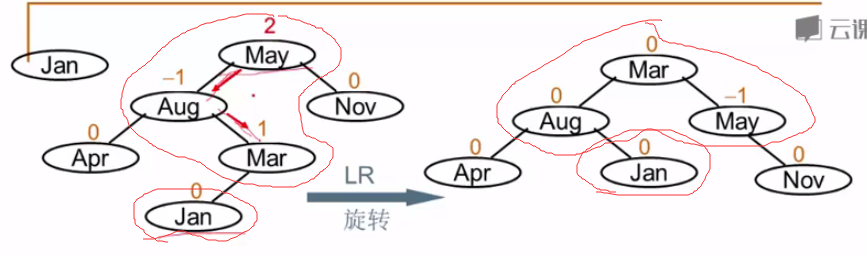
4.RL型破坏：
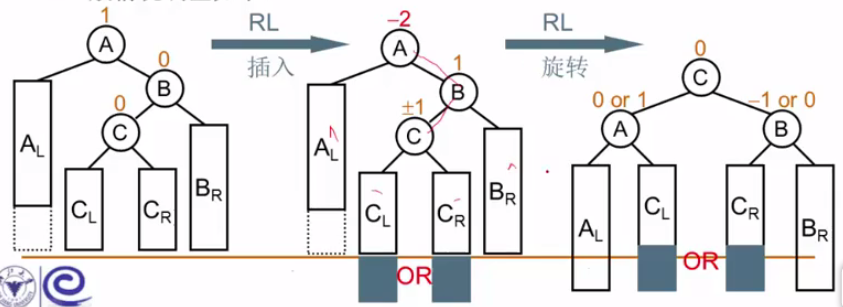
类似LR型破坏，即破坏者位于被破坏者的右子树的左子树（具体放左右无所谓），然后选择关键三个的节点，将中间值得节点拎上来，最左最右子树位置不变，根据大小调整CL,CR的位置。
具体例子：
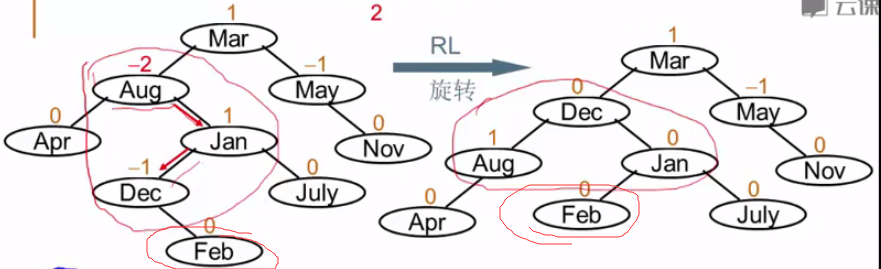
总结：平衡二叉树的思路，就是找寻平衡被破坏的节点（BF>2）,然后沿着破坏的类型寻找关键的三个节点，将其进行旋转，即将中间值得节点拎到中间，然后调整子树的位置，最左边最右边子树不动，根据节点大小将中间的子树调整到对应的位置。
